Cátedra iDanae: Deep Learning

En el ámbito de la Inteligencia Artificial, la disciplina del Aprendizaje Automático o Machine Learning trata de resolver problemas complejos a través de la aplicación de técnicas y algoritmos que permiten extraer información a partir de grandes volúmenes de datos, generados por los sistemas reales que se pretenden analizar. Muchos de estos problemas se pueden resolver a través de algoritmos relativamente sencillos. No obstante, existen múltiples casos complejos en los que se han de aplicar técnicas avanzadas, por ejemplo, debido a la dificultad de la tarea que se ha de desempeñar, o por la complejidad de la función que se desea representar. Tal es el caso de la visión por computador, el procesamiento de audio, el procesamiento del lenguaje natural, algoritmos de búsqueda complejos, etc. 

En estos casos, se puede utilizar un conjunto de técnicas que han resultado ser útiles para resolver estas u otras tareas, y que se agrupan bajo la denominación de aprendizaje profundo o Deep Learning. Esta disciplina puede definirse como “una solución que permite al ordenador aprender de la experiencia en términos de una jerarquía de conceptos, donde cada concepto se define a través de su relación con conceptos más sencillos. […] El gráfico que representaría cómo estos conceptos se construyen sobre cada uno de ellos es profundo, con muchas capas”. 

En general, la representación de las arquitecturas de Deep Learning se realiza a través de las denominadas redes neuronales: representaciones donde la información de entrada se combina en múltiples capas a través de pesos o parámetros y de funciones específicas para obtener un resultado determinado. El Deep Learning se puede entender por tanto como una evolución de algunas técnicas específicas de aprendizaje automático. A pesar de que las técnicas de Deep Learning se comenzaron a establecer en la segunda mitad del siglo XX, su desarrollo se ha visto potenciado en las últimas décadas debido a la mejora del rendimiento de las soluciones obtenidas, la mayor disponibilidad de datos utilizados para el entrenamiento (derivados de mejores procesos de captura, sensorización, etc.), y la mayor capacidad tecnológica para explotar dichos datos y entrenar estructuras con una enorme cantidad de parámetros.

Esta disciplina se nutre de diversos campos de conocimiento para la obtención de redes neuronales: los métodos estadísticos (para el análisis de los datos de partida sobre los que se realizará el entrenamiento, la detección de posibles sesgos y limitaciones, o la comprensión de los resultados obtenidos), el álgebra lineal (aplicada en la representación de la arquitectura de coeficientes o en la implementación de algunos algoritmos), las técnicas de cálculo (puesto que los parámetros se obtienen como resultado de la búsqueda del mínimo de funciones de error), o las ciencias de la computación (que permite abordar la programación de procesos complejos a través del uso de librerías y algoritmos ya implementados que permiten un uso sencillo y optimizado). 

El uso de las redes neuronales presenta un conjunto de ventajas en términos de aplicabilidad y computación:
 

• Las redes neuronales son flexibles y pueden utilizarse tanto para problemas de regresión (continuos) como de clasificación (discretos). Cualquier dato que pueda hacerse numérico puede utilizarse en el modelo, ya que la red neuronal utiliza funciones de aproximación.
• Las redes neuronales funcionan bien en el modelado de datos no lineales con gran número de entradas, por ejemplo, imágenes.
• Una vez entrenadas, las redes pueden realizar predicciones con bastante rapidez.
•  Las redes neuronales pueden entrenarse con cualquier número de entradas y capas, lo que permite obtener una capacidad de representación teóricamente ilimitada (es decir, son aproximadores universales de funciones).
• Las redes neuronales funcionan bien con grandes conjuntos de datos y con buena densidad en el espacio de probabilidad: son capaces de aprovechar gran parte de la información disponible dada la capacidad paramétrica.

No obstante, existen también diversos riesgos asociados al uso de redes neuronales y su implantación en las organizaciones que se deben considerar. Entre otros, la necesidad de disponer de grandes volúmenes de datos de calidad para el entrenamiento de múltiples parámetros, el posible sobreajuste a los datos que puede llevar a la pérdida de capacidad de generalización, o la dificultad de interpretar el modelo o sus resultados, dada la complejidad de las relaciones que se obtienen. Estos retos se exploran en la última sección de este documento.

Existen múltiples tipos de redes neuronales, cada una de las cuales se puede aplicar a diferentes problemas: redes perceptrón multicapa, autoencoders, redes convolucionales, recurrentes, etc. A continuación, se revisan los principales conceptos de esta disciplina, se exponen distintos procesos de entrenamiento de estos modelos, y se analizan distintas arquitecturas que pueden utilizarse para la resolución de problemas.

Redes Neuronales

Concepto y componentes

Conceptualmente, se suele establecer un paralelismo entre los modelos y algoritmos objeto de estudio del Deep Learning, las denominadas redes neuronales artificiales, y las redes de neuronas biológicas, entendidas como conjuntos de elementos (neuronas) que se encuentran conectados entre sí, formando una estructura de red. Esta estructura permite a cada neurona comunicarse y “transmitir información” a través de sus conexiones con otras neuronas, dando lugar a comportamientos complejos que se pueden interpretar como inteligentes.

Una red neuronal artificial puede por tanto conceptualizarse como un conjunto de variables que se combinan a través de unos pesos y actúan como entradas de las distintas neuronas. En cada neurona se aplica una función matemática, denominada función de activación, que produce una salida. Dicha salida puede funcionar a su vez como una nueva variable de entrada para otra neurona, combinándose así la información en distintas capas, hasta obtener una solución final.

El modelo más sencillo sobre el que se fundamentan las neuronas artificiales modernas es conocido como modelo neuronal de McCulloch-Pitts (McCulloch, Pitts 1943). Este modelo se basa en la premisa de que se puede imitar parte de los procesos biológicos mediante una función que recibe una lista de señales de entrada ponderadas por pesos, y emite algún tipo de señal si la suma de estas entradas ponderadas alcanza un determinado umbral.

Este modelo fue el primero en introducir el concepto de neurona artificial y sólo cuenta con dos tipos de entradas, las “excitatorias” y las “inhibitorias”. Las entradas excitatorias tienen pesos de magnitud positiva y las inhibitorias tienen pesos de magnitud negativa. Las entradas de la neurona McCulloch-Pitts pueden ser 0 ó 1 y se sirven de una función de umbral como función de activación donde la señal de salida es 1 si la entrada es mayor o igual que un valor umbral dado, y 0 en otro caso. Sin embargo, esto no permite ajustar toda la gama intermedia de comportamientos que facilita el ajuste y con propiedades matemáticas deseables como, por ejemplo, la diferenciabilidad, esenciales para para posibilitar el entrenamiento. 

Un enfoque más actual consiste en cambiar ciertos aspectos del modelo McCulloch-Pitts, para permitir la conexión de múltiples capas sin perder las propiedades matemáticas deseadas para poder entrenarlas. En lugar de funcionar como un interruptor que sólo puede recibir y emitir señales binarias, las neuronas artificiales modernas utilizan valores continuos con funciones de activación continuas. Por tanto, las neuronas bajo este modelo son funciones de la forma y=f(x,w,b), donde x representa a las variables de entrada, w representa a los pesos o parámetros, b representa al sesgo (valores aditivos constantes, y representan una entrada adicional en la siguiente capa que siempre tendrá el valor de 1), y f es la función de activación.

Para mantener el rango de valores de las neuronas acotado se utilizan las funciones de activación. Estas funciones añaden no linealidad a las funciones de salida que modelan, lo que permite a las redes neuronales construir superficies multidimensionales complejas capaces de ajustarse a problemas no lineales (de hecho, una red neuronal sin función de activación es esencialmente un modelo de regresión lineal).

Extendiendo la expresión de la neurona simple al caso de múltiples capas que transmiten información entre ellas, se obtiene una estructura donde las salidas de una capa (representadas por y) se corresponden con las entradas de la siguiente (representadas por x), que son transformadas por los pesos y sesgos de cada neurona. De esta manera el conjunto de pesos puede ser representado como una matriz n × m (m neuronas de la capa por n entradas de información correspondientes con las n neuronas de la capa previa).

Entrenamiento de las RRNN

En esencia, el entrenamiento de una red neuronal consiste en encontrar los parámetros que minimizan la función que mide el error de la predicción sobre un conjunto de datos: la función de coste. Para ello, se aplican distintos algoritmos y técnicas de optimización, que se exponen a continuación.

La función de coste

La función de coste se define como una agregación, en general por la media, de funciones de pérdida que miden los errores cometidos para cada muestra: Una función de coste, notada por J(w,b,X,ytrue), es una medida del error entre el valor que predice el modelo y el valor real. Esta función será la directriz utilizada para monitorizar el rendimiento de la red y ajustar sus parámetros de forma automática e iterativa mediante los algoritmos de optimización.

Se pueden definir multitud de funciones de pérdida según la tipología del problema y las características de la variable dependiente, aunque usualmente se suelen emplear estimadores máximo-verosímiles (como la LogLoss, conocida como Binary Crossentropy para problemas binarios, Categorical Crossentropy para problemas multiclase u otras funciones de pérdida como el Mean Squared Error [MSE] para problemas de regresión). En todo caso, estas funciones pueden ser cualquier medida de error que tenga buenas propiedades de diferenciabilidad, esencial para entrenar el modelo de forma automática.

Algoritmos de optimización: Backpropagation

La optimización, en contextos de Deep Learning, es el proceso de cambiar los parámetros del modelo para mejorar su rendimiento. En otras palabras, es el proceso de encontrar los mejores pesos en el espacio de hipótesis predefinido para obtener el mejor rendimiento posible. No existen métodos analíticos para entrenar las redes neuronales (salvo en los casos más sencillos compuestos por una sola neurona), por lo que para abordar el problema se emplean algoritmos de optimización numérica.

Para entrenar la red se comienza propagando el error a la capa de salida hasta llegar a la capa de entrada pasando por las capas ocultas (en caso de haberlas). Este proceso de propagación del error se denomina propagación hacia atrás o backpropagation.

El algoritmo de backpropagation tiene como objetivo determinar la contribución de cada parámetro a la función de coste. Para hacerlo se emplea la regla de la cadena del cálculo diferencial, que permite determinar cada una de estas contribuciones como un producto de derivadas. Las derivadas de cada parámetro en cada capa deben ser precalculadas para determinar los gradientes de la hipersuperficie generada por la función de coste.

Por tanto, el algoritmo de backpropagation puede definirse como el conjunto de pasos utilizados para actualizar los pesos de la red con el fin de reducir el error de la misma. Es eficiente en memoria en la búsqueda de soluciones en comparación con otros algoritmos de optimización, como por ejemplo algoritmos genéticos, lo cual es relevante ante estructuras grandes. Además, este algoritmo es lo suficientemente general como para funcionar con diferentes arquitecturas de red.

Optimizadores

Como se ha indicado, para obtener una solución posible al problema se utilizan técnicas de optimización numérica: de forma iterativa se trata de obtener el valor de los parámetros que mejoran el objetivo de minimización.

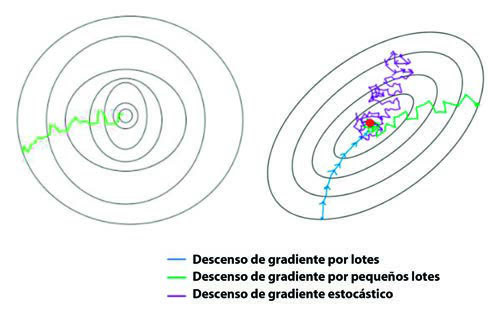
El proceso de búsqueda de un mínimo en la función J(w,b,X,ytrue) comienza en un punto arbitrario en el espacio determinado por los parámetros iniciales. En cada iteración se actualizan los pesos, con el objetivo de aproximarse a un punto que reduzca el valor del error. Este proceso se le conoce como descenso del gradiente y es una de las técnicas de optimización más utilizada dado que puede ser aplicada en la mayoría de algoritmos de aprendizaje.

Cuando se dispone de un sistema o proceso estocástico (es decir, el sistema o proceso está conectado a una probabilidad aleatoria, en este caso determinada por las diferentes observaciones de la muestra), se puede utilizar el conocido como método del descenso del gradiente estocástico, o Stochastic Gradient Descent (SGD), donde se seleccionan aleatoriamente muestras en lugar de todo el conjunto de datos para cada iteración.

Otros tipos de descenso gradiente, como Batch Gradient Descent o Mini-batch Gradient Descent tratan de corregir la regularidad de las oscilaciones al computar la función de coste y las actualizaciones de pesos, lo que aporta robustez al estimador y se obtienen caminos más directos hacia los mínimos.

El ajuste de los pesos en cada iteración vendrá determinado por la pendiente/derivada en el punto evaluado y un factor multiplicativo de esta pendiente, que se introduce como un hiperparámetro del modelo conocido como learning rate.

El método SGD es el más sencillo y general que se puede plantear para actualizar los parámetros de la red, sin embargo, se han propuesto multitud de algoritmos de optimización que permiten explotar diferentes características de los tipos de espacios que generan las redes neuronales artificiales, y que por tanto mejoran la velocidad, eficiencia y convergencia del entrenamiento (como AdaGrad, RMSprop, AdaDelta, Adam, etc.)

Inicialización de los pesos

El rendimiento de una red neuronal depende mucho de cómo se inicializan sus parámetros cuando se comienza a entrenar: si se hace de forma aleatoria para cada ejecución, es probable que no sea reproducible o no tenga un buen rendimiento. Por otro lado, si se utilizan valores constantes, podría tardar demasiado en converger. La inicialización determinará el punto de partida sobre el espacio de la función de error, por lo que es relevante adaptar los valores de los pesos iniciales a las características del espacio para partir de zonas cuyos gradientes sean lo más próximo a las zonas de alta convexidad.

Las técnicas más frecuentes para inicializar los pesos son la inicialización por cero, la inicialización aleatoria, la inicialización de Xavier (trata de evitar la reducción o el aumento de las magnitudes de las señales de entrada de forma exponencial causadas por la composición de los gradientes), o la  Inicialización de He (que persigue el mismo objetivo que la inicialización Xavier, sin embargo, este método muestra un mejor desempeño con algunas funciones de activación). 

Overfitting

Uno de los problemas en el entrenamiento de redes neuronales es el denominado sobreentrenamiento u overfitting: en lugar de aprender un mapa general de entradas a salidas, el modelo puede aprender los ejemplos de entrada específicos y sus salidas asociadas. Esto dará lugar a un modelo que funcione bien en el conjunto de datos de entrenamiento y mal en los nuevos datos por un efecto de memorización, sin poder de generalización. Para evitar este problema se aplican técnicas que limiten la capacidad del modelo sin perder poder predictivo. Entre las más utilizadas cabe destacar las siguientes:

• Gaussian noise: La introducción de ruido en la entrada de una red neuronal puede considerarse una forma de creación de ejemplos sintéticos (data augmentation) ya que aumenta el número aparente de observaciones diferentes de la red. Por tanto, la adición de ruido a los datos de entrada de una red neuronal durante el entrenamiento puede, en algunas circunstancias, conducir a mejoras significativas en el rendimiento de la generalización. Añadir ruido significa que la red es menos capaz de memorizar las muestras de entrenamiento porque están cambiando continuamente, lo que resulta en pesos de red más pequeños y una red más robusta que tiene un menor error de generalización.
• Regularización L2: a menudo se denomina weight decay, ya que hace que los pesos sean más pequeños. También se conoce como Ridge regression y es una técnica en la que la suma de los parámetros al cuadrado, o los pesos de un modelo (multiplicados por algún coeficiente) se añade a la función de pérdida como un término de penalización que también debe minimizarse.
• Regularización L1: denominada Lasso Regression (Least Absolute Shrinkage and Selection Operator), añade el "valor absoluto de la magnitud" del coeficiente como término de penalización a la función de pérdida.
• Dropout: empleándose trata de una técnica de eliminación probabilística de neuronas. Durante el entrenamiento, un cierto número de salidas de las capas se ignoran o se "descartan" aleatoriamente. Esto tiene el efecto de hacer que la capa sea tratada como una capa con un número diferente de nodos y por lo tanto diferente conectividad a la capa anterior. Cada actualización de una capa durante el entrenamiento se realiza con una "vista" diferente de la capa configurada.

Arquitectura de las redes neuronales

En esta sección se pretende dar una visión de algunas de las estructuras de redes neuronales más comunes, desde la estructura más básica (el perceptrón multicapa), a redes neuronales más complejas: autoencoders, como extensión del perceptrón, las redes neuronales recurrentes, y las redes convolucionales.

Redes neuronales perceptrón multicapa 

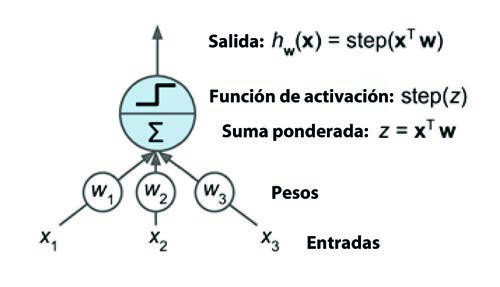
En primer lugar, es conveniente analizar la unidad mínima que compone este tipo de redes neuronales: el perceptrón. Esta estructura tiene un conjunto de datos de entrada, y una neurona de salida (véase figura 4). 
Los inputs introducidos al perceptrón tienen un flujo lineal y unidireccional: las entradas están conectadas directamente a las salidas a través de una serie de ponderaciones. Este tipo de arquitectura se denomina feedforward, porque las conexiones entre las unidades no forman un ciclo. Intuitivamente, esta estructura es análoga a una regresión: cada variable lleva un peso asociado y la suma de todas ellas resulta en una salida, que puede ir asociada a una función de salida.

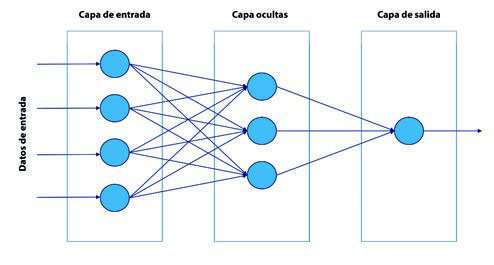
Esta estructura se puede ampliar a múltiples capas con múltiples neuronas en cada capa, lo que da lugar a las redes neuronales perceptrón multicapa.

 
La inclusión de mayor complejidad a la red mediante la adición de capas ocultas permite aumentar su capacidad predictiva en problemas no lineales. Este hecho posibilita a las redes neuronales resolver problemas mucho más complejos y competir con otros modelos avanzados. No obstante, la extensión de la arquitectura y el consecuente aumento de la capacidad predictiva llevan asociados un incremento del coste computacional.

Un caso especial puede considerarse cuando la función de activación es la función ReLU(x) = max(0,x). En este caso, se habla de redes ReLU, y tienen características especiales (son más fáciles de interpretar, puesto que este tipo de redes son funciones continuas lineales a trozos).

Autoencoders 

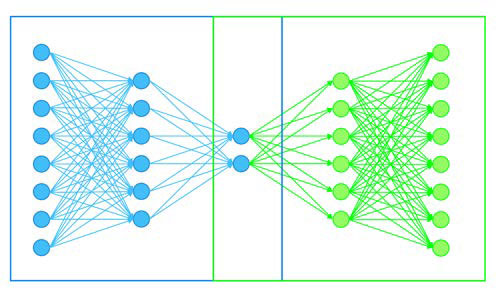
Un autoencoder funciona de forma análoga a una red neuronal perceptrón multicapa, si bien la distribución de las neuronas en las capas ocultas y la capa de salida se organizan de forma diferente. La red se organiza en un codificador, una parte común (véase figura 6, cuadro en rojo) y un decodificador.

De forma simplificada, la red pretende establecer una relación entre dos conjuntos a través de una transformación biunívoca (una función biyectiva). Esto se consigue gracias a la aplicación de capas intermedias con un menor número de neuronas. De forma visual, se puede entender el codificador como un embudo de datos que se encarga de reducir la información introducida en el conjunto de salida. Esta agrupación final del codificador será la entrada inicial de datos del decodificador, que se encargará, a través de las capas intermedias, de volver a reconstruir el dato inicial.

Este tipo de redes pueden utilizarse para reducir la dimensionalidad de un determinado grupo de datos genérico, en la eliminación del ruido, en la detección de anomalías, o en la encriptación de la información, entre otros.

Redes neuronales recurrentes (RNN)

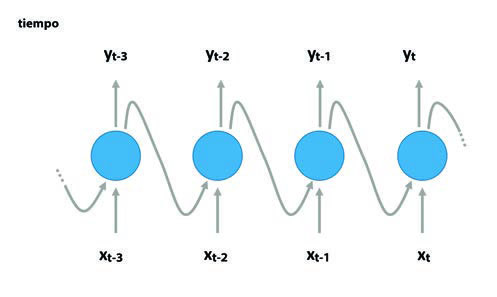
Estas redes se basan en una arquitectura que permite el tratamiento de los datos temporales, mediante la persistencia de la información a lo largo del tiempo. Las RNN consideran el tiempo como variable que modifica un determinado ente. Este hecho hace realmente útil este tipo de arquitecturas para poder obtener características interesantes de datos secuenciales.

Cada neurona tiene como entrada dos inputs: el input inicial para cada unidad temporal y el output de la neurona adyacente. La existencia de estos ciclos en las neuronas permite la persistencia de la información de estados previos. Esta información puede ser usada para poder definir los pasos futuros.

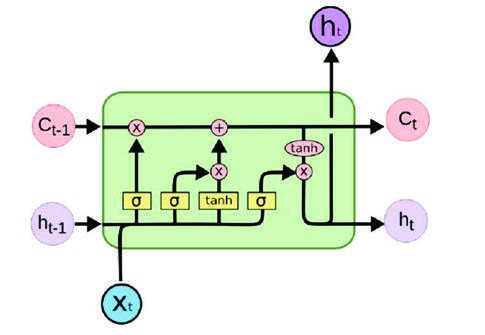
Una de las arquitecturas clásicas de este tipo de RNN son las LSTM (long short-term memory), que tienen la capacidad de mantener la memoria a largo plazo. Este algoritmo dispone de una “puerta” que se encarga de desechar aquella información persistente que ya no resulta útil para definir los siguientes pasos futuros. Estas puertas se entrenan para detectar qué datos son importantes en la secuencia y que, por tanto, deben conservarse, y cuáles deben eliminarse. Posteriormente, puede pasar información relacionada a lo largo de la secuencia de cadena larga para la predicción.

Gracias a la característica de memoria a largo plazo, esta arquitectura resulta especialmente útil para ser utilizada en comprensión de textos o en predicción de series temporales. Si bien es cierto que existen métodos que realizan bien esta función, estos algoritmos tienen la ventaja de que incorporan el contexto y orden de las palabras como información predictiva.

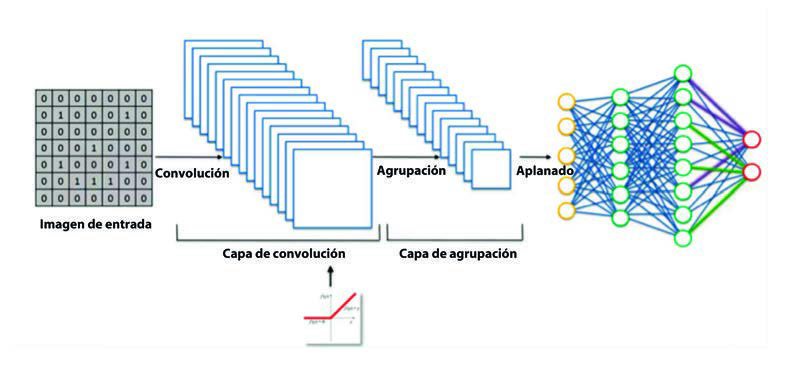
Redes convolucionales

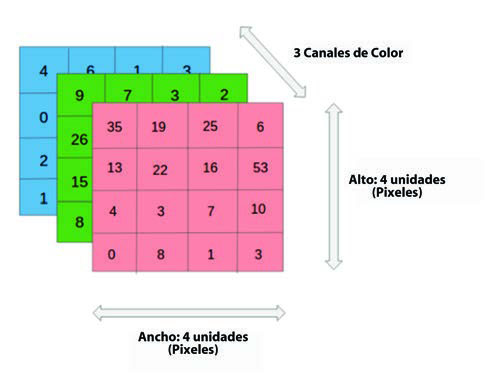
Una de las arquitecturas que juega un papel fundamental en la visión por computador son las redes convolucionales. En el caso del tratamiento de imágenes, los datos de entrada tienen un formato completamente distinto: se trata de píxeles de una imagen, que se distribuyen de forma tridimensional debido a los tres canales RGB (red, green y blue). A diferencia de los datos tabulares, se consideran datos espaciales por el hecho de que un píxel es una magnitud de un punto en una escena. Dos píxeles próximos corresponden a puntos cercanos en una escena, por lo que tendrán valores parecidos.

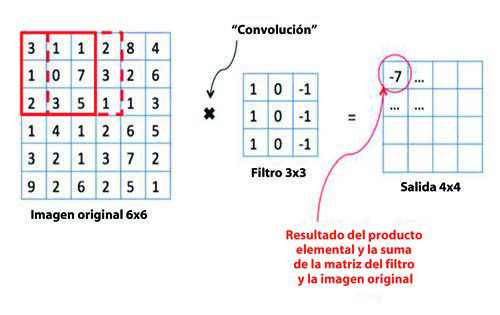
La arquitectura es una variación de un perceptrón multicapa que introduce capas convolucionales. En la primera capa convolucional, cada neurona tiene un recinto asociado en la imagen, una función f. Dicha función se solapa con marcos adyacentes de neuronas que pertenecen a la primera capa convolucional, esto es, una función g. Esta superposición, es aprovechada por el operador convolución para obtener una función h = f * g que en cierto modo resuma la información proporcionada con la imagen. Estas regiones consideradas son de dimensión constante para cada neurona.

Deep Learning Frameworks

La construcción de las arquitecturas de redes neuronales desde cero puede ser un trabajo demasiado tedioso, por lo que hoy en día existe una gran variedad de frameworks que permiten desarrollar modelos de Deep Learning de una forma más rápida y sencilla, sin necesidad de entrar en el detalle del algoritmo subyacente.

Estos marcos de aprendizaje profundo proporcionan componentes prediseñados y optimizados para diseñar, entrenar y validar modelos a través de una interfaz de programación de alto nivel. El mantenimiento de un framework no es una tarea sencilla (de hecho, algunos de ellos no son mantenidos por sus desarrolladores). Por ello, se recomienda que, de cara a seleccionar un marco de Deep Learning, se prioricen aquellos que están en desarrollo activo.

A continuación, se exponen algunos de los frameworks más utilizados:
 

• Tensorflow: se trata de uno de los frameworks de Deep Learning más populares gracias a su potencia y a su facilidad de uso, ofreciendo varios niveles de abstracción en la creación y entrenamiento de modelos. Es compatible con una gran variedad de lenguajes de programación, siendo Python el lenguaje más utilizado. Cabe destacar que el lanzamiento de Tensorflow 2.0 ha incluido numerosos cambios en aras de mejorar la productividad, la simplicidad y la facilidad de uso. 
• Keras: es una biblioteca de código abierto escrita en Python que se creó con el objetivo de proporcionar una rápida experimentación con redes neuronales, pudiendo ejecutarse sobre diversos frameworks de Deep Learning. Se caracteriza por su simplicidad y sencillez, por lo que se considera una muy buena alternativa de cara a iniciarse en el Deep Learning.
• PyTorch: se trata de un framework de Deep Learning que ha adquirido gran importancia en los últimos años, sobre todo en el ámbito académico, convirtiéndose en el principal competidor de Tensorflow. Pytorch se diseñó con el objetivo de acelerar el pipeline completo, desde la creación de prototipos hasta el despliegue en producción, promoviendo un entrenamiento distribuido escalable y una optimización del rendimiento.
• MXNet: Es un framework de Deep Learning flexible, escalable y rápido, que tiene soporte en múltiples lenguajes de programación; destacando su funcionalidad de entrenamiento distribuido. No obstante, en comparación a los frameworks anteriores, su popularidad es mucho menor.

Estos frameworks de Deep Learning se utilizan comúnmente tanto en entornos de investigación como de producción. Además, en consonancia con la popularidad adquirida por la computación en la nube, es habitual su uso en entornos cloud, ya que permiten aprovechar las ventajas que ofrece: disponibilidad de los grandes avances en términos de infraestructura tecnológica (GPUs, TPUs, etc.), escalabilidad o reducción de costes, entre otros.

Retos y oportunidades de la integración de las redes neuronales

Los algoritmos de aprendizaje profundo representan una vía prometedora de investigación para la extracción automatizada de patrones en datos complejos. Estos algoritmos desarrollan una arquitectura jerárquica en capas de aprendizaje y representación de datos, donde las características de nivel superior (más abstractas) se definen en términos de características de nivel inferior (menos abstractas). Las soluciones de aprendizaje profundo han arrojado resultados sobresalientes en diferentes aplicaciones, como el reconocimiento de voz, la visión por computadora, procesado de imagen o el procesamiento del lenguaje natural.

A pesar de los prometedores resultados obtenidos con el uso de Deep Learning, existen diversos desafíos aún por resolver, a los que se enfrenta tanto la comunidad científica como empresas e individuos que usen esta tecnología:

• Volumen de datos: En las redes multicapa completamente conectadas es necesario estimar correctamente un alto volumen de parámetros de la red (en ocasiones, del orden de millones). La base para lograr este objetivo es disponer de una gran cantidad de datos. No obstante, el recopilar un conjunto tan grande de casos anotados (casos donde se ha definido una etiqueta que los identifica, sobre la cual se realiza el aprendizaje), en muchos casos, resulta una tarea compleja. Para solucionar este problema se han utilizado distintos enfoques, consistentes tanto en aumentar el volumen de datos de forma artificial como en mejorar las metodologías de estimación, o una combinación de ambos (por ejemplo, destacan el data augmentation, sparse annotation,  transfer learning, Patch-Wise Training o el Weakly Supervised Learning).
• Calidad de los datos: la escasez de datos, la redundancia y los valores nulos o los conjuntos no equilibrados son desafíos de calidad de la información en los procesos de modelización. En el caso de conjuntos de datos no equilibrados (unbalanced datasets), la clase anómala (minoritaria) suele ser la clase que se quiere aprender (por ejemplo, en el ámbito de detección de fraude, la clase minoritaria es precisamente la presencia de fraude). El entrenamiento de una red con estos datos a menudo lleva a que la red entrenada esté sesgada y puede que se quede en los mínimos locales de la función de coste. Se pueden usar varios métodos para mejorar la calidad de los datos, incluida la limpieza de datos, normalización de datos, selección de características, o reducción de dimensionalidad, entre otros.
• Temporalidad y datos no estáticos: En múltiples dominios de conocimiento (como el médico, el financiero o la fabricación) es necesario analizar la evolución a lo largo del tiempo. El diseño de enfoques de aprendizaje profundo que puedan manejar datos temporales es un aspecto importante que requerirá el desarrollo de soluciones novedosas.
• Sobreajuste y tiempo requerido para el entrenamiento de los modelos: estos retos vienen derivados de la necesidad de utilizar grandes volúmenes de datos. Por lo tanto, cualquier solución que pueda aumentar el tamaño de los datos también puede ayudar a resolver el problema de sobreajuste. Asimismo, reducir el tiempo de aprendizaje y conseguir una convergencia más rápida son temas centrales de múltiples estudios.
• Interpretabilidad: en muchos sectores y ámbitos de conocimiento (como en el financiero) es relevante entender qué factores subyacen a una clasificación. Conseguir la interpretabilidad es crucial para generar confianza y que se fomente el uso de herramientas de soporte a la decisión basadas en este tipo de modelos.

Todos estos desafíos, no obstante, presentan oportunidades y posibilidades futuras de desarrollo e investigación: 

• Enriquecimiento de los datos: para entrenar los modelos es necesario aumentar no solo el número de individuos de los que extraer características sino también el propio número de características. El desarrollo actual de la tecnología ha hecho posible el almacenamiento de fuentes de datos heterogéneas que se han de integrar y explotar. Una posible solución podría no solo integrar los datos y entrenar un modelo, sino también tratar de ampliar el número de capas, donde cada una de ellas se entrene a partir de datos provenientes de distintas fuentes (demográficas, redes sociales, comportamiento, etc.).
• Análisis federado de los datos y swarm learning: cada organización almacena, explota y gestiona sus propias bases de datos. En muchos sectores, el uso e integración de múltiples bases de datos procedentes de distintas organizaciones podría proporcionar mejores resultados en el entrenamiento de los modelos. No obstante, dicho entrenamiento tendría que realizarse sin filtrar información confidencial entre las organizaciones. Las arquitecturas de aprendizaje federadas y el swarm learning permiten entrenar modelos de redes en un entorno federado, incluyendo una capa de seguridad adicional basada en tecnología blockchain. 
• Privacidad de los modelos: finalmente, la privacidad es una preocupación importante, especialmente en entornos donde los modelos de predicción se implantan como un servicio en la nube. Existen líneas de investigación destinadas a eliminar las vulnerabilidades de este tipo de servicios.

Conclusiones

El aprendizaje profundo se ha aplicado ampliamente en problemas como la visión por computador, el procesamiento del lenguaje natural, o el reconocimiento audiovisual. Adicionalmente, la proliferación de startups y nuevas empresas de servicios tecnológicos ha provocado la incorporación del uso del aprendizaje profundo en múltiples sectores, como el caso de los servicios financieros ante la aparición y el desarrollo de las Fintech. 

Uno de los retos a los que se enfrenta el desarrollo de este tipo de modelos es el tratamiento de datos no estáticos, lo cual es común en sectores como el financiero. Aunque aún existe un amplio recorrido de implantación de modelos de Deep Learning en muchos sectores, probablemente este tipo de algoritmos puede mejorar el conocimiento de los clientes, la recomendación de productos, la mejora de los servicios, la eficiencia de los procesos, o la gestión de la estructura de capital, lo que llevaría a maximizar el valor de las corporaciones.

Por tanto, se ha de continuar investigando para afrontar los diversos retos que surgen en los distintos sectores en relación al desarrollo de herramientas y plataformas que incluyan las técnicas analizadas para la implantación de modelos de Deep Learning. 

La newsletter “Modelización por componentes​" ya está d​​isponible para su descarga en la web de la Cátedra tanto en español como en inglés​.​​