Newsletter trimestral de la Cátedra iDanae: Causal Machine Learning

En este contexto, una de las líneas de trabajo que desarrolla la Cátedra es el análisis de las metatendencias en el ámbito de Analytics. Una metatendencia se puede definir como un ámbito de interés en un campo de conocimiento determinado que requerirá de inversión y desarrollo por parte de gobiernos, empresas y la sociedad en general en un futuro próximo.

En este informe trimestral se ha abordado la causalidad en el ámbito de los modelos de Machine Learning y su impacto en el desarrollo de dichos modelos.

Introducción

Las técnicas de Machine Learning están resultando ser de una gran utilidad y aplicación para el entorno empresarial, lo que explica el importante desarrollo y crecimiento que están teniendo. En el ámbito del aprendizaje automático existen diferentes problemas: algunos están orientados a la búsqueda de patrones, sesgos de conducta, comportamientos, etc., mientras que otros persiguen realizar una predicción concreta.

En este segundo tipo de problemas suele existir una causa, o bien un conjunto de causas que constituyen un sistema causal, y que explican un determinado resultado. Por tanto, es importante conocer y comprender dicho sistema.  Sin embargo, las técnicas de Machine Learning no están desarrolladas para descubrir o comprender las relaciones de causalidad. Se entiende por causalidad a la relación de causa y efecto, de forma que la ocurrencia de un evento (la causa) tiene como efecto que se suceda otro evento. Así, las técnicas de Machine Learning no están diseñadas para entender esta relación causa –efecto. Por ejemplo, estas técnicas podrían detectar una correlación entre el hecho de que llueva y que las personas lleven paraguas, pero no asociar que el segundo hecho es una causa directa del primero. A consecuencia de ello, y debido a la necesidad de poder entender los modelos y las predicciones realizadas por estos para poder generalizar su uso y desarrollar nuevas aplicaciones, la investigación en torno a la causalidad dentro del ámbito de Machine Learning es un tema que está cobrando cada vez más importancia.

La investigación en torno a la causalidad no está exenta de debate, e incluso el propio concepto de causalidad se encuentra sujeto a controversias dentro de la comunidad científica. En el ámbito académico se encuentran tanto investigaciones que renuncian por completo al uso de este concepto, argumentando que es imposible determinar las causalidades, como otras que argumentan que la capacidad de pensar causalmente supone uno de los principales factores de la inteligencia humana que ha permitido el progreso de la civilización, y lo postulan también como un pilar básico y fundamental para lograr avanzar en el desarrollo de inteligencias artificiales.

Dentro del ámbito del Machine Learning, cuando se abordan problemas que se basan en un sistema causal, por ejemplo ante problemas de predicción, una de las suposiciones clave en las que se basan las técnicas desarrolladas es la hipótesis de que si es posible comprender el pasado será posible predecir el futuro.

Esta comprensión, sin embargo, debe ser causal: una comprensión no causal genera un proceso de sobreajuste u overfitting, en el que un modelo aprende sobre el pasado de una forma perfecta, pero es incapaz de detectar las relaciones causales que se mantendrán a lo largo del tiempo y que le permitirán predecir el futuro.

Un ejemplo sencillo que ilustra lo anterior puede ser el siguiente: considérese un sistema de Inteligencia Artificial que trata de aprender a dejar platos sobre una superficie, y su campo de pruebas es una habitación con una mesa de metal y un suelo de parqué. Tras muchos intentos, el sistema acabará encontrando una relación: si deja el plato sobre la mesa el plato no sufre daños, pero si lo suelta donde no hay mesa, el plato cae hasta el suelo y se rompe. Esto resulta trivial si se piensa causalmente. Sin embargo, si sólo se analizan los patrones obtenidos en su proceso de aprendizaje, el sistema puede asociar la rotura del plato a la ubicación de la mesa, o a que el suelo sea de madera, y por tanto predecir que el plato se romperá si la mesa cambia de sitio, o bien si es de madera. Esto puede solucionarse entrenando con diferentes ubicaciones, o con distintos tipos de materiales de la mesa y el suelo, pero si después de ese nuevo entrenamiento se coloca una repisa, nuevamente el sistema no sabrá qué ocurrirá. Necesita un razonamiento causal que le permita generalizar la información obtenida de sus experimentos.

Pese a unos tímidos comienzos a lo largo del siglo XIX, el estudio de la causalidad no comenzó a desarrollarse formalmente hasta hace unas pocas décadas, por carecer de unas herramientas y un lenguaje específico que permitiera su investigación como campo propio5. La aplicación de esta rama de la ciencia a la Inteligencia Artificial pretende conseguir unos modelos con (i) una capacidad de generalización mucho mayor que la actual y (ii) la posibilidad de descartar relaciones espurias y sesgadas:

• El incluir en la modelización la compresión de las causas subyacentes permite generalizar los patrones encontrados en conjuntos de datos de entrenamiento sobre conjuntos de datos nuevos, aunque estos difieran sensiblemente sobre los de entrenamiento. 
• La información obtenida de los datos a través de modelos de Machine Learning es, a priori, más objetiva que los posibles análisis realizados por los seres humanos6. Esto permite, por tanto, una toma de decisiones más adecuada y justa. Sin embargo, los datos de entrenamiento de estos modelos pueden contener sesgos ocultos para los desarrolladores, lo que puede llevar a decisiones injustas sobre determinados individuos con base en variables de carácter sensible (género, raza, orientación sexual, etc.). Entender cómo, y especialmente, por qué una variable sensible influye sobre otras variables en los datos de entrenamiento resulta fundamental para eliminar los sesgos. Por ejemplo, un modelo puede asociar una mayor correlación entre la aparición del cáncer de pulmón y el ser hombre, cuando la verdadera causa subyacente podría estar relacionada con los recursos económicos disponibles. Esto puede evitarse mediante una comprensión causal de los patrones encontrados en los datos. 

Descripción de la causalidad

El problema de la correlación y la causalidad

Uno de los primeros aspectos que se aborda en el análisis de la causalidad es su diferenciación frente al fenómeno de correlación. Desde un punto de vista formal, se entiende que una variable A causa la variable B si y solo si al menos un elemento del par (A,¬A) causa al menos un elemento del par (B,¬B)8. La causalidad es transitiva (si A causa B, y B causa C, entonces puede decirse que A causa C), irreflexiva (un evento A no puede causarse a sí mismo) y antisimétrica (si A causa B, entonces B no es una causa de A). La correlación, por otro lado, es una medida estadística que identifica asociaciones entre variables. Algunas de estas relaciones podrán tener una interpretación causal, pero la medida de la correlación no puede determinar por sí sola si efectivamente existe una relación causal. En caso de relación de correlación, esta no determina qué variable es la causa y qué variable es el efecto. La correlación entre dos variables refleja el grado de predictibilidad cruzada entre ambas. 

débil que una causalidad. Mientras que la causalidad de una variable sobre otra se determina unívocamente a través una única relación entre los eventos (X→Y), la correlación entre dos variables permite la existencia de diversas relaciones entre estos. Puede llegar a darse el caso de la existencia de correlaciones espurias, que son situaciones en las que dos variables se encuentran correlacionadas sin tener ningún tipo de relación causal.

En una publicación anterior ya se introdujeron las diferencias entre correlación y causalidad y los problemas que se generan a la hora de modelar y realizar predicciones. La existencia de una correlación entre dos variables no implica una causalidad entre ellas, pudiendo incluso invertirse la correlación al introducir el efecto de una tercera variable (lo que se conoce como paradoja de Simpson). La distinción entre correlación y causalidad resulta, por tanto, fundamental como paso preliminar antes de abordar el análisis de la causalidad. Es por ello que dentro de la investigación de la causalidad se establece un marco de tres niveles donde poder categorizar los sistemas inteligentes en función de su capacidad para determinar relaciones causales.

Los tres niveles de causalidad

El establecimiento de un marco para analizar la capacidad causal de un sistema inteligente (ya sea una Inteligencia Artificial o un organismo) permite identificar tres niveles de capacidad. Cada nivel corresponde a una capacidad mayor, pudiendo solucionar los problemas que en un nivel previo resultan imposibles. Estos niveles son:

Nivel de asociación: en esta etapa se incluyen las tareas de observación y búsqueda de patrones. Es el nivel de la correlación. La mayoría de los seres vivos se encuentran en este nivel, así como todos los sistemas de Inteligencia Artificial que se han desarrollado en la actualidad. Un ejemplo de este nivel sería el de un ratón que al pulsar un botón recibe una descarga eléctrica y deja de hacerlo.

Nivel de intervención: en esta fase se incluye el comprobar la existencia de una causalidad a base de cambiar uno de los elementos del sistema, dejando el resto constante. Sólo algunos animales se encuentran en este nivel.  Un ejemplo de este nivel sería el realizar un estudio sobre la efectividad de un medicamento administrando la cura a un conjunto de pacientes y un placebo a otro conjunto de características similares.

Nivel contrafactual: esta etapa se caracteriza por la capacidad de abstracción. La comprensión de las herramientas utilizadas es mayor, lo que permite entender por qué funcionan y cómo actuar cuando no lo hacen. En este nivel se encuentra el ser humano. Un ejemplo de este nivel sería la capacidad humana para desarrollar teorías científicas.

Para conseguir desarrollar sistemas de Inteligencia Artificial con una capacidad predictiva mucho mayor que la conseguida actualmente, es necesario dotar a estos sistemas de herramientas para que puedan modelar la causalidad. Esto no sólo repercutirá en su desempeño, sino que además permitirá que estos sistemas sean más robustos, adaptables e interpretables. Para conseguir esto, la aproximación clásica ha sido diseñar experimentos para obtener relaciones de causalidad en entornos controlados para comprobar una determinada hipótesis, como por el ejemplo el uso de grupos de control; mientras que la aproximación bayesiana, que es más utilizada en el ámbito de Machine Learning, ha consistido en el desarrollo de las redes Bayesianas.

Modelos causales

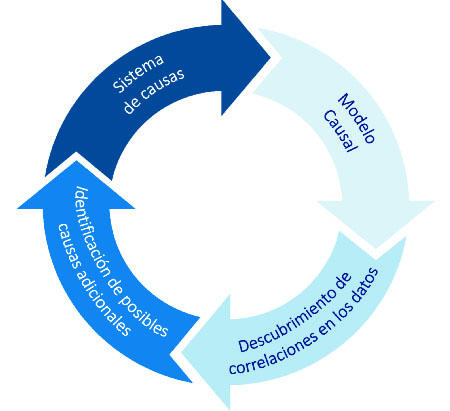
Como se ha expuesto, en aquellos problemas en los que se pretende encontrar un sistema causal que explica un resultado, es importante incorporar conjuntamente modelos causales con modelos de Machine Learning. Esta incorporación puede realizarse de forma cíclica: Un modelo que explica un sistema de causas (determinista) puede integrarse con un modelo de Machine Learning, que a partir de los datos detecte patrones y correlaciones. Estos patrones pueden ser explicados por parte del sistema causal, y por tanto pueden dar lugar a la identificación de nuevas causas, que a su vez se pueden incorporar en el modelo determinista. Por ello, es importante disponer de sistemas de big data que permitan analizar todos los datos producidos para la búsqueda de dichas correlaciones.

Por ejemplo, si se produce una caída de un sistema informático que puede afectar a toda una organización, es importante analizar el sistema de causas que ha llevado a este evento, y eso se puede realizar mediante el estudio de datos procedentes de servidores, comunicaciones, routers, conexiones, usuarios, etc. Una vez que se analizan estos datos, se pueden completar los modelos causales que permiten explicar la caí­da de dicho sistema y, por tanto, poder evitar posibles caí­das en el futuro.

La creación de un modelo causal permite describir el mecanismo causal del sistema en estudio. Esto facilita la investigación del sistema y puede llegar a evitar la realización de algunas pruebas o experimentos de campo. Un modelo causal está formado por dos elementos: (i) unas ecuaciones estructurales, compuestas por un conjunto de variables endógenas y un conjunto de variables exógenas; y (ii) un conjunto de funciones que determinan el valor de las variables endógenas en función del resto de variables endógenas y exógenas, que cuenta con un grafo asociado, conocido como red Bayesiana.

Redes Bayesianas

El teorema de Bayes se ha utilizado ampliamente en el campo de la inferencia probabilística. Sin embargo, a la hora de inferir probabilidades entre variables que no están directamente relacionadas entre sí, o para un gran número de variables, el procedimiento, aunque posible, se vuelve tedioso, al mismo tiempo que su coste computacional se incrementa debido al aumento en el número de conexiones. Para solucionar estas dificultades se desarrollaron a principios de los años 80 las redes Bayesianas. Estas redes encapsulan las dependencias condicionales entre las variables mediante la realización de un grafo acíclico dirigido, donde las aristas del grafo representan las influencias directas entre las variables. Las ecuaciones estructurales se asocian al grafo al identificar cada nodo con los conjuntos de variables endógenas y exógenas y las aristas con el conjunto de funciones.

La conexión entre los grafos y las distribuciones de probabilidad de los eventos viene dada por la condición de Markov, en la que se establece que cada nodo en una red Bayesiana es condicionalmente independiente de todos los nodos que no están conectados con el propio nodo. Desde un punto de vista causal, esto implica que un nodo es independiente de todas las causas o efectos directos del propio nodo. Esta conexión, gracias a la condición de Markov, hace que las redes Bayesianas sean especialmente útiles para predecir la probabilidad de que ocurra una de las posibles causas para un evento dado.

Modelos causales en Inteligencia Artificial

La utilización de un modelo causal permite solucionar varios de los problemas existentes actualmente en el desarrollo de sistemas de Inteligencia Artificial debido a los siguientes motivos:

• Interpretabilidad: la capacidad de sistematizar los supuestos causales permite la creación de modelos más transparentes, de forma que el usuario pueda analizar estas asunciones y determinar si son plausibles o no, o si es necesario añadir nuevas asunciones.
• Formalización contrafactual: los modelos de ecuaciones estructurales y las representaciones gráficas permiten sistematizar el razonamiento contrafactual, lo que permite determinar mejor las causas y los efectos.
• Transmisión de cambios: esto permite transmitir los cambios de las variables causa a la variable efecto, permitiendo además identificar variables intermedias, de forma que la aparición de este tipo de variables supone la transmisión del efecto entre otras dos.
• Adaptabilidad y validez: el conocimiento causal de los patrones en los datos permite a los sistemas adaptarse a situaciones sobre las que no tienen experiencia porque no han sido entrenados sobre ellas, permitiendo obtener modelos más robustos.
• Datos faltantes: en los modelos causales es posible determinar relaciones aún incluso aunque existan datos faltantes cuando se cumplan unas determinadas condiciones, lo que permite producir estimaciones consistentes.
• Descubrimientos causales: por último, la consecución de unas relaciones causales que puedan ser desconocidas hasta el momento, mediante la presentación de conjuntos de los posibles modelos causales que se ajustan a los datos de entrenamiento, permite obtener nuevas variables explicativas en el modelo.

Conclusiones

El estudio de la causalidad ha tenido un desarrollo muy reciente, no siendo hasta hace unas pocas décadas cuando se ha formalizado como campo de estudio. El desarrollo de modelos causales basados en las ecuaciones estructurales y las redes Bayesianas han dado un gran impulso en la investigación de la causalidad, suministrando herramientas de gran potencia en la identificación de relaciones causales y que permiten además una modelización sencilla.

En la resolución de problemas que presentan un objetivo de predicción y que se basan en la existencia de sistemas de causas, el incorporar la capacidad de realizar descubrimientos causales parece un requisito relevante para lograr el objetivo a largo plazo de conseguir una verdadera Inteligencia Artificial. En el corto plazo, esta capacidad permitirá obtener unos modelos de Machine Learning más robustos, generalizables e interpretables, que podrán enfrentarse mejor a situaciones desconocidas diferentes de los datos con los que han sido entrenados. Un mayor conocimiento causal, y por tanto una mayor interpretabilidad, además, permitirá un mayor uso de estos modelos en sectores regulados o para realizar funciones alrededor de las cuales existen actualmente diversos debates éticos.

La newsletter “Causal Machine Learning" ya está disponible para su descarga en la web de la Cátedra tanto en español como en inglés​.​​