Newsletter trimestral de la Cátedra iDanae: Algoritmos de Machine Learning
La Cátedra iDanae (inteligencia, datos, análisis y estrategia) en Big Data y Analytics, creada en el marco de colaboración de la Universidad Politécnica de Madrid (UPM) y Management Solutions, publica su newsletter trimestral correspondiente al 1T21 sobre Algoritmos de Machine Learning
Cátedra iDanae: Algoritmos de Machine Learning
Introducción
En los últimos años, el auge de la Inteligencia Artificial, el Aprendizaje automático o Machine Learning, y el Aprendizaje profundo o Deep Learning, se ha incorporado a todas las industrias y sectores.
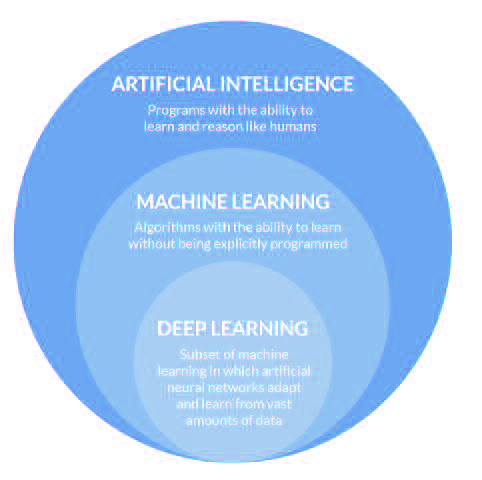
Estos tres términos suelen usarse indistintamente como sinónimos. Sin embargo, conceptualmente se puede considerar que la Inteligencia Artificial es el campo más amplio en el que se pueden enmarcar las otras disciplinas.
Más concretamente, la Inteligencia Artificial es un área de la computación que estudia cómo lograr que las máquinas realicen tareas propias del ser humano, es decir, intenta simular el comportamiento inteligente. Por otra parte, el Machine Learning se puede considerar un subcampo de la inteligencia artificial que permite a los ordenadores aprender de los datos sin estar programados explícitamente para ello, pudiéndose ver como una posible metodología de cara a dotar a un sistema inteligente de la capacidad de realizar una determinada tarea. Así, el Machine Learning puede definirse como el conjunto de métodos que pueden detectar patrones automáticamente en un conjunto de datos y usarlos para predecir datos futuros, o para llevar a cabo otro tipo de decisiones en entornos de incertidumbre.
Por último, el Deep Learning también permite a los ordenadores aprender de los datos, pero se basa en el uso de complejas redes neuronales, de varias capas, donde el nivel de abstracción aumenta gradualmente mediante transformaciones no lineales de los datos. Dentro de este marco, la presente newsletter se centra en la disciplina del Machine Learning.
El auge de este área conlleva múltiples debates en torno a los principales desafíos que presenta, como pueden ser la capacidad para modelar la causalidad, la aproximación empresarial en el uso de este campo desde un punto de vista ético, organizativo, etc., así como otros elementos técnicos como la calidad de los datos, su insuficiencia o no representatividad, la capacidad computacional necesaria, entre otros. Adicionalmente a dichos elementos, y como fundamento de la disciplina, surge también la necesidad de entender los algoritmos de aprendizaje en los que se basa este campo de conocimiento. Por ello, en esta newsletter se pretende dar una visión general sobre los algoritmos de Machine Learning más utilizados, con el objetivo de aportar una base de conocimientos para el correcto uso de los diferentes algoritmos.
Tipos de algoritmos
Dentro de los algoritmos de Machine Learning, existen diferentes categorizaciones de acuerdo a distintos criterios: grado de supervisión durante el entrenamiento, posibilidad de llevar a cabo un aprendizaje incremental, forma de generalización, etc. Cabe señalar que estas clasificaciones no son necesariamente estáticas, ya que en algunos casos se han incorporado nuevas ramas como consecuencia de la aparición de nuevas técnicas cuya naturaleza no permitía clasificarlas con ninguna de las categorías existentes.
En primer lugar es necesario realizar una distinción, basada en la funcionalidad, entre algoritmos descriptivos y predictivos, siendo una categorización extendida dentro del campo de la minería de datos. Un algoritmo descriptivo tiene como objetivo describir la población mediante la exploración de las propiedades y características de los datos, mientras que un algoritmo predictivo tiene como objetivo realizar predicciones sobre eventos futuros desconocidos a partir de datos históricos. A su vez, cada categoría se puede desglosar en varias subcategorías, lo que permite una clasificación más detallada de los algoritmos. En el caso de los algoritmos descriptivos se pueden encontrar las subcategorías (1) clustering, (2) summarization, (3) reglas de asociación y (4) sequence discovery; mientras que, en el caso de los algoritmos predictivos, se encontrarían (1) clasificación y (2) estimación de valor.
Sin embargo, hoy en día, es más común utilizar una clasificación basada en la tipología de datos disponibles, es decir, de acuerdo a si se dispone de datos etiquetados o no etiquetados. Se pueden distinguir cuatro categorías:
Aprendizaje supervisado: los algoritmos de aprendizaje supervisado intentan modelar las relaciones existentes entre los datos de entrada y la variable objetivo, de forma que se puedan predecir los valores de la variable objetivo para datos nuevos en función de las relaciones aprendidas a partir de datos históricos etiquetados. Para inferir estas relaciones, los conjuntos de entrenamiento utilizados deben incluir los valores de la variable objetivo, llamados comúnmente “etiquetas”.
Hay dos tipos principales de aprendizaje supervisado:
- Clasificación: su objetivo es predecir la pertenencia a una determinada clase, por ejemplo, determinar si un correo es spam o no. Por tanto, la variable objetivo es discreta (generalmente, se trata de un conjunto finito de clases).
- Estimación de valor: su objetivo es predecir un valor numérico, por ejemplo, el precio de venta de una casa. Por tanto, la variable objetivo suele ser continua (aunque la predicción final puede ser un conjunto discreto de valores representados por un indicador, como, por ejemplo, la media de un grupo).
Aprendizaje no supervisado: los algoritmos de aprendizaje no supervisado permiten inferir patrones o relaciones existentes en conjuntos de datos sin etiquetar. Al contrario que en el aprendizaje supervisado, no se predice un valor objetivo (no se dispone de etiquetas), sino que se exploran los datos y se realizan inferencias que permitan descubrir estructuras ocultas en los datos.
Se pueden destacar los siguientes tipos de algoritmos de aprendizaje no supervisado (lista no exhaustiva):
- Clustering: su objetivo es encontrar grupos o clusters de individuos o variables similares existentes en los datos, por ejemplo, grupos homogéneos de clientes para llevar a cabo una segmentación comercial.
- Aprendizaje de reglas de asociación: su objetivo es descubrir relaciones entre las variables, extrayendo reglas y patrones a partir de los datos; por ejemplo, para determinar patrones de consumo.
- Otros algoritmos: existen múltiples algoritmos que no se pueden encuadrar en las categorías anteriores; algunos de ellos se utilizan con frecuencia en otros procesos, como sería el caso de los algoritmos de reducción de dimensionalidad y detección de anomalías, utilizados habitualmente en el preprocesamiento de los datos. Debido a su utilización en fases distintas al entrenamiento del modelo propiamente dicho, estos algoritmos no se tratarán en esta newsletter.
Aprendizaje semisupervisado: se trata de un enfoque híbrido entre el aprendizaje supervisado y no supervisado. En este caso, los datos de entrenamiento son conjuntos parcialmente etiquetados, donde unos pocos ejemplos están etiquetados y una gran cantidad de ejemplos no lo están. El objetivo de estos algoritmos es hacer un uso efectivo de todos los datos disponibles, no solo de los etiquetados. Estos modelos se emplean cuando el etiquetado de los datos puede llevar mucho tiempo, ser demasiado costoso, o no está disponible para parte de la muestra.
Aprendizaje por refuerzo: engloba aquellos problemas en los que un agente aprende a operar en un entorno mediante un proceso de retroalimentación (es decir, prueba y error). El objetivo de estos algoritmos es utilizar la información obtenida de la interacción con el entorno para llevar a cabo aquellas acciones que maximicen la recompensa o minimicen el riesgo; se trata de un aprendizaje iterativo mediante la exploración de las distintas posibilidades. No se dispone de un conjunto de datos de entrenamiento, sino de una meta que el agente ha de lograr, un conjunto de acciones que este puede realizar y retroalimentación sobre su desempeño.
Bajo esta categorización, en los siguientes apartados se ahondará en los principales algoritmos correspondientes a las categorías de aprendizaje supervisado y no supervisado, pues son los más comúnmente utilizados hoy en día.
Algoritmos supervisados y no supervisados
En este apartado, se proporciona una breve visión de los principales algoritmos de aprendizaje supervisado y no supervisado que pueden utilizarse de cara a abordar la resolución de un problema. La elección del modelo dependerá tanto del tipo de datos como del tipo de la tarea a realizar, siendo fundamental la validación del modelo.
Aprendizaje supervisado
Tal y como se expuso en el apartado anterior, los algoritmos de aprendizaje supervisado intentan modelar las relaciones existentes entre los datos de entrada y la variable objetivo. En función de si la variable objetivo es discreta o continua, se tratará de un problema de clasificación o estimación de valor, respectivamente.
Entrenamiento del modelo
En términos generales, un algoritmo de aprendizaje supervisado construye un modelo a partir de modelos patrón, examinando un conjunto de ejemplos e intentando encontrar los parámetros que minimicen o maximicen una función objetivo, comúnmente denominada función de pérdida. De este modo, los parámetros o pesos del modelo se irán ajustando iterativamente con el objetivo de aproximarse al óptimo de dicha función.
Más detalladamente, la función de pérdida se utiliza como una medida del buen funcionamiento del modelo en términos de su poder predictivo. Hay varios factores involucrados en la elección de esta función, pero existe una diferenciación clara según el tipo de tarea que se vaya realizar, estimación de valor o problemas de clasificación.
Entre las funciones de pérdida de estimación de valor, una de las más utilizadas es el error cuadrático medio (MSE), calculado como el promedio de la diferencia cuadrática entre las observaciones reales y las predicciones, representándose mediante la siguiente ecuación:
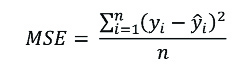
De este modo, esta función mide la magnitud promedio del error, independientemente de su dirección.
Por otra parte, una de las funciones de pérdida de clasificación más utilizadas es la entropía cruzada, que mide el rendimiento de aquellos modelos cuya salida es un valor de probabilidad entre 0 y 1. Matemáticamente se puede formular mediante la ecuación:
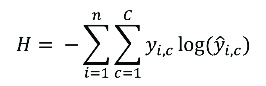
El valor de esta función aumentará a medida que la probabilidad predicha difiera de la etiqueta real, penalizando fuertemente las predicciones que sean seguras, pero erróneas.
Rendimiento del modelo
El rendimiento es un factor clave a la hora de elegir el modelo. Un buen modelo de clasificación no debería ajustarse exclusivamente a los datos con los que ha sido entrenado, sino que debería funcionar correctamente sobre nuevas instancias nunca antes vistas. Esta segunda parte hace referencia a la capacidad de generalización del modelo. Por tanto, se distingue entre error de entrenamiento (calculado sobre el conjunto de datos con el que fue entrenado el modelo) y error de validación o de test (calculado sobre un conjunto de datos independiente, que no se usó en el entrenamiento).
Así, se dice que el modelo tiene un buen rendimiento si el error de validación se mantiene acotado, y en el mismo orden de magnitud que el error de entrenamiento. Por tanto, el error de validación es una buena forma de medir el rendimiento del modelo. Para su estimación, debido a que los datos suelen ser limitados, se suele recurrir a utilizar el método hold-out, a partir del cual se divide el conjunto de datos en los subconjuntos de entrenamiento y test. Sin embargo, otra alternativa más robusta para estimar este error es la validación cruzada, método mediante el que se divide el conjunto de datos en k grupos, se utilizan k-1 grupos para entrenar y uno para testear el modelo.
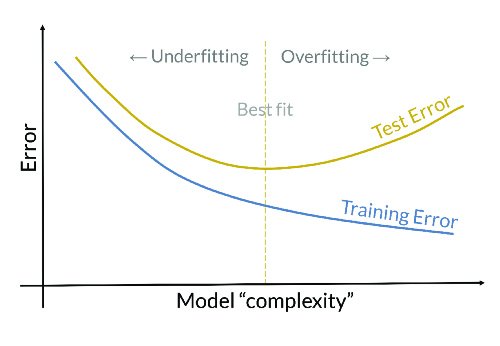
Si el error de generalización fuera significativamente mayor que el error de entrenamiento, el modelo estaría sobreajustando los datos de entrenamiento, lo cual implica que el modelo no es capaz de generalizar bien sobre datos nuevos. Esta situación se denomina overfitting, y su probabilidad de ocurrencia aumenta a medida que aumenta la complejidad del modelo. Por ello, de acuerdo al principio de la navaja de Ockham, entre dos modelos con el mismo error de validación, se seleccionará el más simple. No obstante, si el error de entrenamiento es muy alto, el modelo no estaría siendo capaz de modelar los datos de entrenamiento, y, por consiguiente, tampoco de generalizar a datos nuevos, denominándose underfitting. En la Figura 2 se pueden observar estas casuísticas.
No obstante, a pesar de la utilización de una metodología común, la forma en la que se evaluarán las predicciones variará en función de si se trata de un problema de clasificación o estimación de valor. A continuación, se exponen las principales medidas utilizadas en cada categoría.
Clasificación
- Matriz de confusión: matriz n x n23, donde las filas hacen referencia a las clases reales y las columnas a las clases predichas, mostrando de forma explícita el nº de instancias de cada clase predichas correctamente y el nº de instancias en el que una clase se ha confundido con otra.
- Accuracy: proporción de predicciones correctas realizadas por el modelo.
- Precision: fracción de predichos clasificados correctamente, es decir, cuántos de los predichos son verdaderamente de la categoría predicha.
- Recall: fracción de ejemplos clasificados correctamente del total de ejemplos de una determinada clase.
- F1-Score: media armónica de las medidas Precision y Recall.
Estimación de valor
- Error cuadrático medio: promedio de la diferencia cuadrática entre las observaciones reales y las predicciones.
- Raíz del error cuadrático medio: raíz cuadrada del promedio de las diferencias al cuadrado entre las observaciones reales y las predicciones.
- R2: proporción de variabilidad explicada por el modelo.
Finalmente, es preciso recordar que la consecución de un buen rendimiento no depende únicamente del algoritmo elegido. Sin un preprocesamiento de los datos no se obtendrán unos resultados precisos, independientemente del algoritmo.
Principales algoritmos
Una vez abordado tanto el entrenamiento como la validación de un modelo, se exponen los principales algoritmos recogidos bajo la categoría de aprendizaje supervisado. No se realiza una diferenciación entre algoritmos de clasificación y de estimación de valores debido a que algunos se podrán utilizar para ambas tareas.
Regresión lineal
Es un enfoque lineal para modelar la relación entre una variable respuesta continua (variable dependiente) y una o más variables explicativas (variables independientes). El caso de una variable explicativa se denomina regresión lineal simple, representándose matemáticamente mediante la ecuación:
Y=a+bX
Donde X es la variable independiente e Y es la variable dependiente. La pendiente es b y el intercept es a, siendo estos los coeficientes del modelo que se ha de estimar, ajustándose habitualmente por el método de mínimos cuadrados. En la siguiente figura, se puede visualizar un ejemplo de regresión lineal simple.
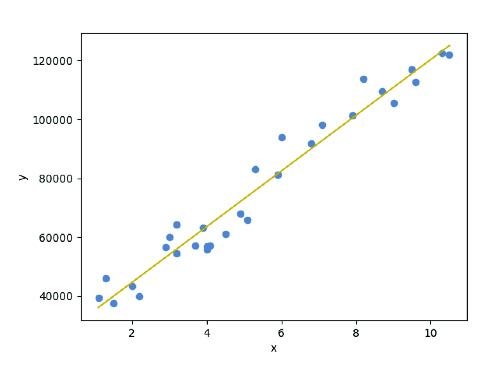
Este modelo suele ser un buen baseline para los problemas de estimación de valor. No obstante, es importante corroborar el cumplimiento de las hipótesis del modelo: (1) linealidad, (2) homocedasticidad, 3) independencia y (4) normalidad.
Regresión logística
Es un método estadístico que se utiliza en problemas de clasificación, prediciendo la probabilidad de ocurrencia de los diferentes resultados posibles. En concreto, este algoritmo busca un hiperplano que sea capaz de separar linealmente las clases.
y= σ(a+bX)
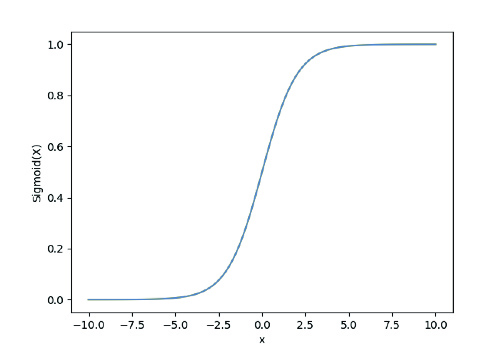
A diferencia de la regresión lineal, la variable dependiente es categórica, es decir, toma un número limitado de valores. Cuando esta variable solo tiene dos valores posibles, se denomina regresión logística simple, prediciendo la probabilidad de ocurrencia de ese evento. Matemáticamente, se formula mediante la ecuación:
Donde σ es la función sigmoide, la cual se encarga de asignar probabilidades a los valores predichos.
Como consecuencia de su simple formulación, este modelo se considera un buen baseline a emplear en problemas de clasificación.
K-vecinos más cercanos (k-nn)
Es un algoritmo de aprendizaje perezoso no paramétrico que se puede usar para resolver tanto problemas de clasificación como de estimación de valor.
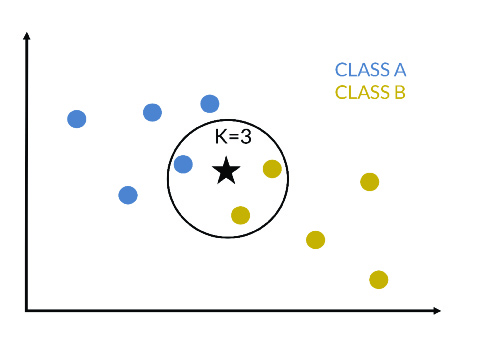
Más concretamente, dada una nueva instancia que se quiere clasificar, se calculan las distancias de este punto respecto a las instancias que conforman el conjunto de entrenamiento, se seleccionan las k-instancias más cercanas y se calcula la media de las etiquetas numéricas (en un problema de regresión) o se selecciona la clase más frecuente (en un problema de clasificación). En la siguiente figura, se presenta un ejemplo de 3-nn, donde la nueva instancia pertenecerá a la clase B.
Su uso generalizado se debe a su buen rendimiento, sencillez y versatilidad; aunque también hay que tener en cuenta sus inconvenientes: (1) dificultad para determinar el k óptimo; (2) necesidad de almacenar el conjunto de entrenamiento; y (3) tiempo de ejecución proporcional al tamaño de los datos.
Árboles de decisión
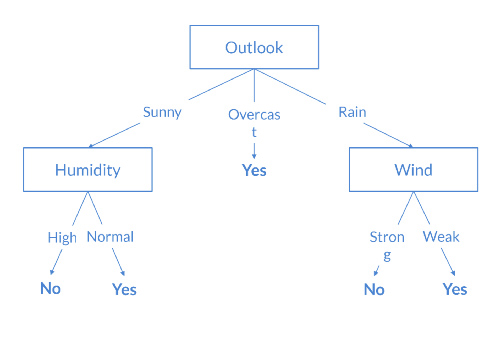
Este algoritmo se basa en la estrategia “divide y vencerás”, utilizándose tanto para problemas de clasificación como de estimación de valor, siendo su objetivo predecir el valor de la variable objetivo a partir de reglas de decisión simples inferidas a partir de los datos. En otras palabras, este algoritmo subdivide el espacio de características en regiones, mapeando cada una de las regiones finales a un valor de la variable objetivo. De este modo, se trata de un modelo simple e interpretable, que proporciona una explicación de los resultados inferidos por el modelo. En la siguiente figura, se puede visualizar un árbol de decisión utilizado en una tarea de clasificación binaria.
Naive Bayes
Es un algoritmo de clasificación que se basa en el teorema de Bayes. Este clasificador supone que las variables son independientes y que cada una contribuye de forma equivalente al resultado. No obstante, estas hipótesis no se suelen satisfacer en problemas reales; el supuesto de independencia rara vez se cumple, pero, aun así, este algoritmo suele funcionar bien en la práctica.
Matemáticamente, mediante el teorema de Bayes, se estable la siguiente relación:
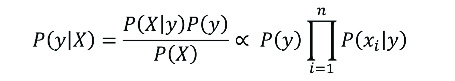
Donde y es la clase y X=(x1,x2,…,xn) el conjunto de características. De este modo, la clase predicha será aquella que presente la mayor probabilidad.
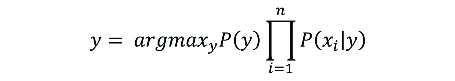
Se trata de una técnica simple y robusta, que tolera de forma satisfactoria los valores missing. No obstante, si una variable categórica tiene una categoría que no se observa en el conjunto de entrenamiento, el modelo asignará una probabilidad de 0 y no se podrá realizar una predicción.
Support Vector Machine
Este popular algoritmo se puede utilizar tanto para tareas de clasificación como de estimación de valor, aunque su uso está más extendido en tareas de clasificación. Su objetivo radica en encontrar un hiperplano, en un espacio N-dimensional, que separe las clases de puntos, transformando para ello las variables explicativas mediante funciones kernel. Estas funciones se utilizan para mapear funciones separables no linealmente en funciones separables linealmente de dimensión superior.
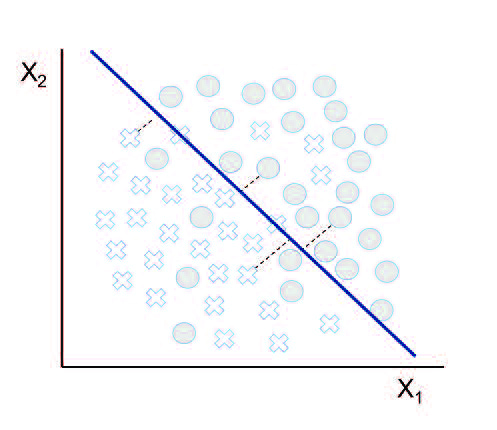
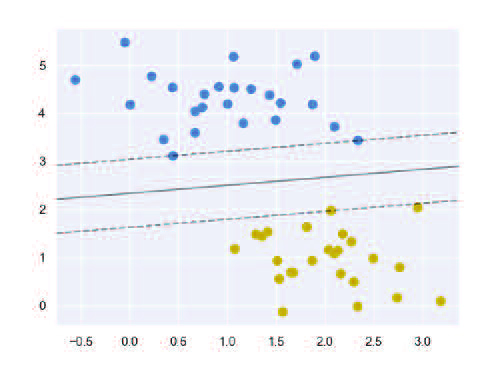
Más concretamente, se debe encontrar el hiperplano en un espacio de dimensión superior al espacio en el que se encuentran los datos que maximice la distancia entre los puntos de datos de as clases (denominada margen). De este modo, se intenta tener un mayor margen de confianza para predicciones futuras. En la siguiente figura, se puede visualizar un ejemplo en el que se representa el hiperplano que separa mejor los datos, y el margen.
De cara a emplear este algoritmo, hay que tener en cuenta que su entrenamiento puede prolongarse bastante en el tiempo si se dispone de un gran conjunto de datos.
Redes neuronales
El incremento de la capacidad computacional, así como el aumento del volumen y tipología de los datos, ha dado lugar a un amplio desarrollo en el ámbito de las redes neuronales, lo que ha propiciado un gran auge de la disciplina Deep Learning.
En este contexto, en el que el procesamiento de los datos no estructurados (texto, audio, imágenes y video) se ha convertido en una importante fuente de información, las áreas de Natural Language Processing y Computer Vision han avanzado rápidamente.
No obstante, debido al elevado número de tipos de redes neuronales existentes y a la complejidad de las mismas, este tipo de algoritmos no se aborda en esta newsletter.
Técnicas para la mejora del aprendizaje. Métodos Ensemble
Los métodos ensemble se basan en la combinación de múltiples modelos en aras de obtener mejores resultados utilizando el conocimiento conjunto, pudiéndose utilizar tanto para tareas de clasificación como de estimación de valor. Hay dos técnicas principales:
- Bagging: los modelos se entrenan en paralelo y la combinación de las predicciones se utiliza como predicción final.
- Boosting: los modelos se entrenan secuencialmente de forma que cada modelo trata de corregir los errores del modelo anterior.
A continuación, se describen brevemente algunos de los métodos ensemble más utilizados:
- Random Forest: este algoritmo de bagging crea varios árboles de decisión de forma paralela y los fusiona combinando sus predicciones para obtener predicciones más precisas y estables.
- Gradient Boosting: como el propio nombre indica, se trata de un algoritmo boosting. Este método combina secuencialmente una serie de árboles, de modo que cada árbol se centre en corregir el error del árbol anterior. Más concretamente, esto se realiza modelando el error de predicción del árbol de decisión anterior. En particular, una implementación específica de este algoritmo es el XGBoost, que trata de mejorar la velocidad de ejecución y el rendimiento del modelo.
- AdaBoost: es un algoritmo similar al anterior, diferenciándose en el modo en el que cada árbol corrige el error del árbol anterior. En este caso, en cada iteración se actualizan las ponderaciones de las observaciones en función de los errores cometidos, es decir, se asigna mayor peso a aquellas observaciones que el modelo no haya sido capaz de predecir correctamente.
Aprendizaje no supervisado
Los algoritmos de aprendizaje no supervisado tienen como objetivo descubrir patrones ocultos en datos sin etiquetar. La ausencia de estas etiquetas supone la ausencia de un punto de referencia con el que evaluar la calidad del modelo, lo que aumenta la complejidad de la validación del modelo. En este apartado, se exponen algunos ejemplos enmarcados en las categorías descritas anteriormente.
Clustering
Estos algoritmos, cuyo objetivo es descubrir agrupaciones naturales en los datos, se basan en la hipótesis de que observaciones pertenecientes al mismo grupo deben tener características similares; y, al contrario, observaciones pertenecientes a distintos grupos deben tener características diferentes. De este modo, este tipo de algoritmos pretenden agrupar los datos de forma que las instancias de un grupo sean similares entre sí (minimizando la distancia intra-grupo) y diferentes respecto a otros grupos (maximizando la distancia inter-grupo).
Existe una gran variedad de algoritmos de clustering, y cada uno de ellos ofrece un enfoque diferente de cara a abordar esta tarea. Las principales categorías en las que se agrupan estos algoritmos son:
- Clustering partitivo: las particiones se generan de acuerdo con una medida de similitud. Ej. k-means, pam.
- Clustering jerárquico: busca construir una jerarquía de clusters, denominada dendograma. Existen dos enfoques claramente diferenciados:
- Aglomerativo (enfoque de abajo hacia arriba): cada observación constituye su propio cluster inicialmente, y se van fusionando de acuerdo a una condición de similitud. El algoritmo suele detenerse cuando se cumple un cierto criterio, con lo que genera varios clusters. Ej. agnes.
- Divisivo (enfoque de arriba a abajo): todas las observaciones se incluyen inicialmente en un único cluster y se realizan divisiones de forma recursiva. El algoritmo suele detenerse cuando se cumple un cierto criterio, con lo que genera varios clusters. Ej. diana.
- Clustering difuso: la asignación de las instancias a cualquiera de los clusteres no es fija, pudiendo una instancia pertenecer a más de un cluster. Ej. fanny, daisy.
- Clustering basado en densidades: los clusters se crean según la densidad de los puntos de datos. Ej. DBSCAN, OPTICS, meanshift.
- Otros: basados en grafos (espectral), basados en modelos probabilísticos (modelos de mixturas), entre otros.
La elección de qué algoritmo se debe emplear es compleja y no inmediata, y es necesaria la experimentación sobre el conjunto de datos. Por tanto, no existe un mejor algoritmo, sino que la adecuación de uno u otro dependerá de la distribución inherente a los datos.
En cualquier caso, es importante cuantificar el rendimiento de la agrupación realizada. En general, se puede distinguir entre medidas extrínsecas, las cuales requieren el conocimiento de las etiquetas verdaderas, y medidas intrínsecas, que miden la bondad de los resultados sin tener en cuenta información externa. De acuerdo con la propia definición de aprendizaje no supervisado, bajo la cual no se disponen de datos etiquetados, en esta newsletter se pone el foco en la validación intrínseca, siendo habitual distinguir entre medidas de cohesión y de separación. Concretamente, las medidas de cohesión determinan el grado de proximidad de los puntos que conforman un cluster, mientras que las medidas de separación determinan el grado de separación de los clusters. Algunas de las medidas intrínsecas más utilizadas son:
- Coeficiente de Silhouette: calculado para cada instancia del onjunto de datos como donde a mide la cohesión como la distancia media de esa instancia al resto de instancias de ese cluster y b la separación como la distancia media de esa instancia al conjunto de instancias que conforman el cluster más cercano. El cálculo de esta medida a nivel de cluster se calculará como la media de este coeficiente para todas sus instancias. Este coeficiente está acotado al intervalo [-1, 1] donde un valor más alto será indicativo de clusters mejor definidos.
- Índice Davies-Bouldin: se calcula como la similitud promedio de cada cluster con su cluster más similar. Cuanto menor sea su valor, mejor será la partición, siendo el valor mínimo de este índice 0.
- Índice de Dunn: se define como la proporción entre la mínima distancia inter-grupo y la máxima distancia intra-grupo. Cuanto mayor sea su valor, mejor será la agrupación.
Finalmente, se exponen algunos de los algoritmos de clustering más utilizados:
- K-means: es probablemente el algoritmo de clustering más onocido y utilizado. Especificando un número de clusters a priori, el algoritmo permite asignar cada observación al centroide más cercano. En particular, se seleccionarán al azar k centroides, y mediante un proceso iterativo se asigna cada punto a su centroide más cercano, actualizando en cada paso el valor de los centroides.
- DBSCAN (density-based spatial clustering of applications with noise): es un algoritmo basado en densidades, es decir, asume la existencia de un cluster cuando identifica una región densa, lo que permite detectar como outliers aquellos puntos que no superan un umbral de densidad establecido. De esta manera, este algoritmo se basa en detectar puntos con densidad suficiente y construir clusters en torno a ellos, añadiendo puntos cercanos al mismo. Para ello, es necesario especificar la distancia máxima para que dos puntos se consideren vecinos y el número mínimo de puntos para conformar un cluster.
En la siguiente figura, se puede visualizar una comparativa de los resultados obtenidos con estos dos métodos sobre distintos conjuntos de datos.
Así pues, se pueden percibir las siguientes ventajas del algoritmo DBSCAN respecto al algoritmo k-means: (1) Puede encontrar clusters con formas geométricas arbitrarias, (2) Tiene capacidad de detectar outliers, (3) No es necesario especificar el número de clusters y (4) Consistencia en sus resultados en diferentes ejecuciones. En contrapartida, el rendimiento del algoritmo k-means es ligeramente mejor gracias a su simplicidad.
La newsletter “Algoritmos de Machine Learning" ya está disponible para su descarga en la web de la Cátedra tanto en español como en inglés.